ADsP 데이터분석 준전문가 - 회귀분석, 회귀 모형의 가정, 회귀 모형의 해석

독립변수(=설명 변수)

다른 변수에 영향 받지 않고 독립적으로 변화하는 수

종속변수

독립변수의 영향 받아 값이 변화하는 수
분석 대상이 되는 변수
결과물이나 효과를 나타냄

잔차(오차항)

계산에 의해 얻어진 이론 값과 실제 관측이나 측정에 의해 얻어진 값의 차이
오차 : 모집단, 잔차 : 표본집단
잔차의 독립성 가정에 대한 검토는 더빈 왓슨 통계량을 이용함

회귀분석

변수와 변수 사이의 관계를 알아보기 위한 통계적 분석 방법
독립변수 값에 의해 종속변수 값을 예측하기 위함
종속변수가 연속형 변수일 때 가능
이산형 - 명목, 서열척도
연속형 - 구간, 비율척도

선형회귀

종속변수 y와 한 개 이상의 독립변수 X와의 선형 상관관계를 모델링하는 회귀분석 기법

단순선형회귀모형

독립변수 1개 일 때
i번째 종속변수 = 선형회귀식 절편 + 회귀계수(coefficient)*i번째 독립변수 + 오차
(예시)
set.seed(2)
X = runif(50, 0, 5) # runif(개수, 시작, 끝) : 시작~끝 범위에서 개수 만큼의 균일분포 따르는 난수 발생
y = 5 + 2 * x + rnorm(50, 0, 0.5) #rnorm(개수, 평균, 표준편차) : 특정 평균 및 표준편차를 가지며 정규분포를 따르는 난수 발생
df <- data.frame(x, y)
fit <- lm(y~x, data=df) #df에서 y를 종속변수, x를 독립변수로 회귀 모형 생성, 다중공선성을 확인할 수 없음
fit
회귀 방정식
y=2072 * x + 4.748

최소자승법

Y=f(X)의 측정값과 함수값의 차이를 제곱한 것의 합이 최소가 되도록 Y=f(X)를 구하는 것
Y=aX+b 일 때 잔차를 제곱한 것의 합이 최소가 되도록 하는 상수 a, b를 찾는 것
큰 폭의 잔차에 대해 보다 더 큰 가중치를 부여함

다중 회귀 모형 예시

회귀모형의 가정

선형성 : 독립변수의 변화에 따라 종속변수도 변화하는 선형 모델이다
독립성 : 잔차와 독립변수의 값이 관련되어 있지 않다(Durbin-Watson 통계량 확인)
정규성 : 잔차항이 정규분포 이뤄야 함
등분산성 : 잔차항들의 분포는 동일한 분산을 갖는다
비상관성 : 잔차들끼리 상관이 없어야 함

Normal Q-Q plot

정규성(정상성), 잔차가 정규분포를 잘 따르고 있는지 확인하는 그래프
잔차들이 그래프 선상에 있어야 이상적

Scale-Location

등분산성, y축이 표준화 잔차를 나타냄
기울기 0인 직선이 이상적

Cook's Distance

일반적으로 1값이 넘어가면 관측치를 영향점으로 판별함. 여기서 영향점은 이상치, 튀는 값 정도로 생각하면 됨

Residuals vs Fitted

선형성, 등분산성에 대해 알아볼 수 있는 그래프

여기서 숫자와 함께 표시된 점은 이상값

Residuals vs Leverage

회귀분석에는 잔차의 크기가 큰 데이터가 outlier가 되는데 이 중에서 주로 관심가지는 것은 Leverage와 Residual 크기가 모두 큰 데이터임
Leverage : 종속변수 값이 예측 값에 미치는 영향을 나타낸 값
Cook's distance : Leverage와 Residual을 동시에 보기 위한 기준
Leverage가 커지거나 Residual의 크기가 커지면 cook's distance 값이 커짐
일반적으로 1 넘어가면 관측치를 영향점으로 판별함

회귀모형 해석(평가방법)

F통계량

모델의 통계적 유의성을 검정하기 위한 검정 통계량(분산 분석)
F통계량 = 회귀제곱평균(MSR) / 잔차제곱평균(MSE)
F통계량이 클수록 회귀 모형은 통계적으로 유의하다 p-value < 0.05일 때 유의함

결정계수

R제곱 = SSR/SST
회귀식의 적합도를 재는 척도
결정계수(R제곱) = 회귀제곱합(SSR) / 총제곱합(SST), 1-(SSE/SST)
SST : Total Sum of Squares, Y의 변동성, SST = SSE + SSR
SSE : Error Sum of Squares, X, Y를 통해 설명하지 못하는 변동성
SSR : Regression Sum of Squares, Y를 설명하는 X의 변동성
결정계수가 커질수록 회귀방정식의 설명력이 높아진다
결정계수는 0~1사이의 범위를 갖는다
회귀계수의 유의성 검증은 t값과 p값을 통해 확인한다

df = n + k -1
n = df - k + 1
41 + 5 + 1 47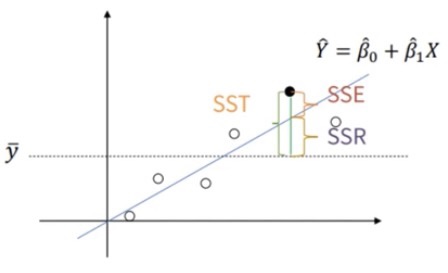

다중회귀모형 해석 예시

만약에 이 데이터에서 샘플의 수가 몇이냐고 물어보면 n = df + k + 1 이기 때문에 46+3+1 = 50이라고 대답하면 됨

통계적 유의성 : F통계량, 유의확률(p-value)
모형의 설명력 : 결정계수
회귀계수의 유의성 : 회귀계수의 t값, 유의확률(p-value)
모형의 데이터 적합성 : 잔차 통계량 확인, 회귀 진단 진행

회귀모형에서 p-value가 2.43e-0.5 같은 형식으로 표현되어 있을때 e-0.5는 10의 -5승 정도라고 생각하면 됨